2.5. Применение ЭВМ при раскрое материалов

До сих пор существующие методы раскроя материалов для изделий из кожи основаны на выполнении одним работником двух групп операций - размещение шаблонов и вырубание (вырезание) деталей. При этом производительность труда и рациональное использование материалов в значительной степени зависят от субъективных качеств каждого исполнителя. Повышение производительности труда ограничивается физическими возможностями рабочего и последовательным способом раскроя.

Современные математические методы и вычислительная техника позволяют решать задачи оптимального размещения деталей на материале, определять прогрессивные нормы использования и потребность в сырье.

Для этого составляются следующие задачи:

1. построение оптимальных модельных шкал (расчет коэффициента укладываемое);
2. формирование схем размещения деталей;
3. оптимизация размеров материала;
4. расчет оптимальных комбинаций моделей для совместного раскроя;
5. расчет оптимального варианта заказа материалов (кожи, искусственные и синтетические кожи), необходимого для выпуска заданного ассортимента деталей и выбора оптимальных вариантов схем размещения;
6. оптимизация целевого использования материалов для деталей низа обуви;
7. расчет потребности в материалах на этапе подготовки производства.

Большой вклад в решение указанных задач внесли Ю. П. Зыбин [3], Г. П. Испирян, С. М. Смирнов, В. А. Скатерной и др.

Основное внимание в работах, связанных с применением ЭВМ при раскрое материалов, уделяется оптимизации схем раскроя, так как от них зависят нормы использования и потребность в сырье [2].

Продолжением и развитием работ по оптимизации схем раскроя материалов с применением ЭВМ явилась методика получения множества экономичных вариантов схем раскроя листовых материалов на детали низа обуви, разработанная в МТИЛП и ЦНИИКП и в настоящее время внедряемая в обувное производство.

Методика состоит из последовательных уровней I-V [4, 5]:

• I - построение множества вариантов размещения и взаимного совмещения абстрактных блоков;
• II - отсев полученных нереальных размещений абстрактных блоков, не отвечающих требованиям рационального раскроя;
• III - получение множества проектных схем на основе выявленных реальных совмещений абстрактных блоков;
• IV - выбор экономичных вариантов схем размещения деталей заданного размерного ассортимента в результате варьирования деталей различных размеров и их количества внутри проектных схем;
• V - получение множества экономичных вариантов схем размещения деталей с помощью варьирования деталей, отличающихся размерами, количеством и углом наклона в исходных блоках относительно краев материала (рис. 2.26).

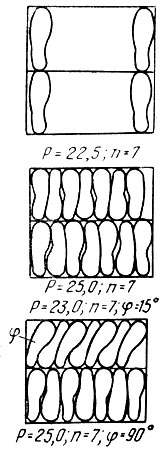
Рис. 2.26. Схема получения множества вариантов раскроя материала

При создании экономичных вариантов схем размещения используется блочная система. Под блоком понимаем совокупность деталей одного размера, наиболее плотно размещенных в заданной прямоугольной области по одной из прямолинейно-поступательных схем. Размеры блока определяются количеством деталей, их размерами, принятым углом наклона осей. Понятие "блок" используется на каждом уровне методики.

Определим понятие "абстрактный блок" I и II уровней методики. Это область с неопределенными габаритными размерами, которая характеризуется местом, занимаемым в матрице, и направлением (вертикальное или горизонтальное) осей деталей, размещенных в ней.

На III уровне применяется термин "проектный блок". Это область с неопределенными габаритными размерами, которая характеризуется местом, занимаемым на листовом материале, и расположением осей деталей в вертикальном или горизонтальном направлении.

В IV уровне исходный реальный блок определяется расположением деталей на листовом материале и характеризуется габаритными размерами, количеством и размерами размещенных деталей, их ориентацией.

В V уровне выходной блок определяется так же, как и исходный, дополнительно ориентированным размещением деталей внутри блока, т. е. фиксированным углом наклона осей относительно краев материала.

При решении задач поиска экономичных вариантов схем раскроя термин "исходный блок" может быть заменен термином "выходной блок".

Под проектными схемами понимаем область без заданных границ, но с указанием размещения проектных блоков. Проектные схемы характеризуются числом размещенных блоков, а также их ориентацией.

Под экономичными схемами, у которых процент использования выше нормативного, понимаем конкретный вариант размещения с указанием размеров листового материала, количества размещенных деталей, их размеров. В экономичных схемах размерный ассортимент не соблюдается.

На I уровне методики без учета границ прямоугольной области создается множество вариантов размещения абстрактных блоков с учетом их взаимного совмещения.

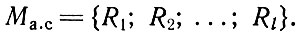
На II уровне методики производится отсев некоторых вариантов совмещения абстрактных блоков с точки зрения технологических требований к создаваемым впоследствии схемам размещения деталей на листовом материале. На этом уровне из М_{а. с} выделяется подмножество реальных вариантов совмещения абстрактных блоков.

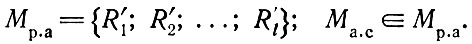
На III уровне организуется переход от множества реальных сочетаний абстрактных блоков Мр. а ко множеству проектных схем, т. е. из

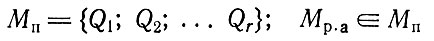
каждого реального совмещения абстрактных блоков строится проектная схема размещения

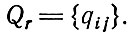
На основе множества проектных схем М_п получается множество экономичных вариантов исходных схем раскроя путем проверки всех возможных сочетаний деталей разных размеров в проектных блоках и выявления сочетаний исходных блоков с наиболее плотными укладками. Критерий отбора - процент использования листового материала. По каждой проектной схеме 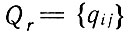строится множество конкретных исходных схем размещения

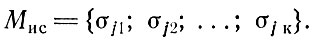
На следующем уровне методики отбираются исходные блоки с малым процентом использования площади блока. Производится поиск более удачного использования площади каждого исходного блока путем размещения деталей большего размера с подбором оптимального угла наклона деталей. На основе σ_j строятся улучшенные схемы σ'_j множество которых

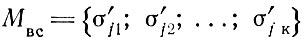
является окончательным результатом применения методики.

Предлагаемая методика направлена на получение максимального процента использования листового материала при заданных размерном ассортименте деталей и габаритных размерах листа, т. е. максимизируется функционал вида

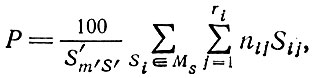
где S_m'S' - общая площадь материала; M_s - множество схем размещения деталей на данной площади; n_ij - число деталей в j-м блоке i-й схемы; S_ij - площадь деталей в j-м блоке i-й схемы.

Особенностью методики поиска экономичных вариантов схем раскроя является поиск лучшего размещения деталей, осуществляемого в два этапа:

1. размещение абстрактных блоков на плоскости без каких-либо конкретных размеров;
2. поиск плотных совмещений деталей на листовом материале с учетом их размеров.

На первом этапе реализуются I-III уровни методики, на втором - IV и V. Уровни I, IV, V выполняются автоматизированно с применением ЭВМ, уровни II и III вручную.

Предложенная методика гарантирует получение множества возможных экономичных вариантов схем раскроя листовых материалов на детали низа обуви.

Рассмотрим решение задачи по трем уровням предложенной методики получения множества экономичных вариантов схем раскроя листовых материалов на детали низа обуви.

I. Создание множества вариантов размещения и взаимного совмещения абстрактных блоков:

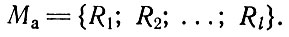
II. Отсев размещений деталей, не отвечающих требованиям рационального раскроя материала:

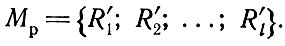
III. Представление множества выделенных совмещений деталей абстрактных блоков в виде проектных схем:

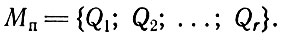
Определим условия задачи по I уровню методики.

Задано некоторое число абстрактных блоков, детали в которых размещены горизонтально, а также некоторое число абстрактных блоков, детали в которых размещены вертикально. Область размещения представлена в виде прямоугольной матрицы размерностью 6×6 клеток.

Требуется получить все множество возможных размещений и взаимного положения (вертикальных и горизонтальных) абстрактных блоков в поле заданной матрицы.

Исходя из предположений, что количество вариантов размещений абстрактных блоков в поле заданной матрицы есть конечное множество, при введении ограничения на число блоков можно формализовать задачу их поиска и получить решение с помощью ЭВМ.

Анализ производственных схем размещения деталей, используемых московским производственным объединением по выпуску деталей низа обуви "Пролетарий", показал, что количество делюжек (блоков), помещающихся на одном листе пластины и отличающихся размерами деталей, их количеством и углом расположения относительно друг друга, как правило, не более пяти. Используя эти данные, введем ограничение: число абстрактных блоков, размещенных одновременно в одной матрице, не должно превышать шести. Схемы, имеющие большее число размещенных блоков, труднореализуемы исполнителями в процессе раскроя и, как правило, не применяются из-за их сложности.

Решение задачи получения множества размещений и взаимного совмещения абстрактных блоков основано на теории графовых грамматик.

Выявление множества размещений абстрактных блоков заключается в следующем. Каждое возможное совмещение абстрактных блоков будет задано матрицей размерностью 6×6 клеток, которая заполнена элементами: 0; -1; +1, где 0 - пустое место; +1, -1 - абстрактные блоки однотипных деталей, расположенных соответственно горизонтально и вертикально.

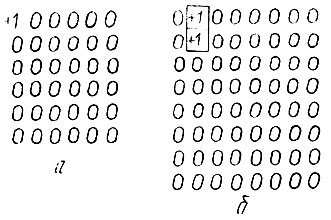
Рис 2.27. Исходная матрица

Примем, что первая исходная матрица состоит из одного блока с единицей в левом верхнем углу (рис. 2.27,а). Из нее строим все возможные матрицы с добавлением одного блока (+1 или -1). Для этого рассматриваем матрицу большего размера (8×8 клеток), в центре которой помещаем исходную матрицу (размером 6×6 клеток) (рис. 2.27, б). В большей матрице поочередно меняем один из нулей на элементы, используя следующие правила. Замена разрешается тогда, когда на одну клетку вверх, вниз, вправо или влево от заменяемого нуля находится отличный от нуля элемент. Это существенно меняет матрицу. Затем полученную матрицу сравниваем со всеми предыдущими. Если она новая, то ее записываем в общий массив возможных матриц, предварительно выделив значащие элементы в поле меньшей матрицы (6×6 клеток).

Найдя все возможные варианты размещения и совмещения двух абстрактных блоков, снова выбираем новую эталонную матрицу уже с двумя абстрактными блоками и производим аналогичную достройку еще одного блока.

Поиск новых матриц размещения абстрактных блоков прекращается тогда, когда число абстрактных блоков, размещенных в одной матрице, начинает превышать шесть, т. е. когда перебраны все возможные варианты размещения.

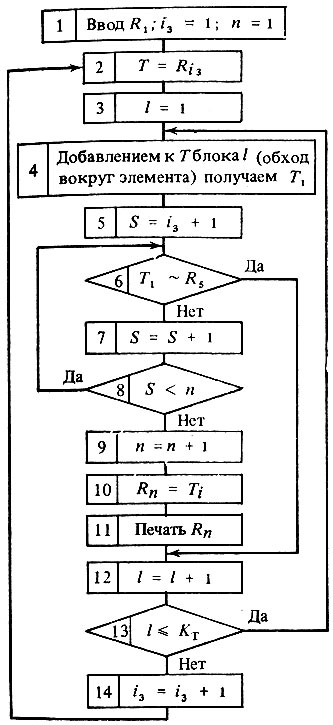
Рис. 2.28. Блок-схема алгоритма получения абстрактных блоков

При принятом ограничении предложенная методика гарантирует получение всего множества вариантов совмещений абстрактных блоков в поле заданной матрицы. На основании описанной методики разработан алгоритм, блок-схема которого приведена на рис. 2.28. Алгоритм реализован в программу на языке Фортран для ЭВМ ЕС-1020. Время выполнения программы на ЭВМ составило 15 мин.

Для реализации полученного множества матриц в проектные схемы размещения разработаны правила, предотвращающие уменьшение числа возможных проектных схем размещения, представляющих практический интерес. Эти правила направлены на заполнение пустых мест в матрице при реализации ее в проектную схему размещения. Правила заключаются в следующем.

1. Горизонтально направленные абстрактные блоки (+1) могут распространяться и заполнять пустые места матрицы только в вертикальном направлении.
2. Вертикально направленные абстрактные блоки (-1) могут распространяться и заполнять пустые места матрицы только в горизонтальном направлении.
3. Пересечение и накладка различных абстрактных блоков при заполнении пустых мест недопустимы.

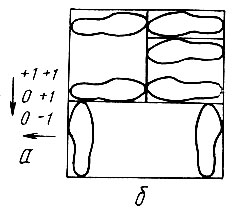
Рис. 2.29. Проектная схема размещения деталей на листовом материале

При применении установленных правил реализация матрицы (рис. 2.29, а) в проектную схему размещения показана на рис. 2.29, б.

ЭВМ производит перебор всех возможных сочетаний, перестановок элементов +1; -1; 0, поэтому получаются такие матрицы, которые по установленным правилам не могут быть реализованы в проектные схемы размещения, а также дающие один и тот же результат (симметрично повторены). Все эти матрицы отбрасываются. С технологической точки зрения реальный интерес представляют 135 проектных схем размещения.

Таким образом, выделено конечное число возможных вариантов проектных схем размещения деталей на листовом материале при принятом ограничении. Полученные результаты используются как исходные данные в следующей программе по расчету экономичных вариантов схем размещения деталей на листовом материале.

Рассмотрим четвертый уровень методики получения экономичных вариантов схем раскроя листовых материалов на детали низа обуви.

Сформулируем задачу. Имеется прямоугольная область Q с заданными габаритными размерами. Задано множество проектных схем m ₁, m₂, ..., m_z, причем каждая из них СОСТОИТ ИЗ Г блоков однотипных деталей. Для рассматриваемого фасона деталей низа обуви задается размерный ассортимент K₁, K₂, ..., K_g. Необходимо, используя заданные проектные схемы размещения m ₁, m₂, ..., m_z, реализовать размерный ассортимент K₁, K₂, ..., K_g с максимальным использованием материалов. Задача будет решаться путем перебора различных комбинаций деталей в проектных схемах размещения.

Рис. 2.30. Блок-схема алгоритма получения экономичных вариантов схем размещения деталей

Разработан алгоритм получения экономичных вариантов схем размещения, укрупненная блок-схема которого представлена на рис. 2.30, а. Введем условные обозначения: a_i - номер детали, размещенной в i-м блоке; r - число блоков; А и В - соответственно длина и ширина листового материала; l и h - соответственно длина и ширина детали α; n_i - число деталей, размещенных в i-м блоке; δ - межшаблонный мостик; S - чистая площадь детали; Н₁ и Н₂ - соответственно первый и второй линейный эффект от совмещения деталей по ширине; Р_п - установленный пороговый процент использования; φ - угол наклона продольной оси детали.

Ознакомимся с принципами, заложенными в представленный алгоритм. В качестве исходной информации используются габаритные размеры листового материала и деталей размерного ассортимента, чистые площади деталей, линейные эффекты от совмещения, а также множество проектных схем размещения, задаваемых в виде прямоугольной матрицы 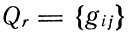, в которой элемент g по модулю равен номеру блока, которому он принадлежит, а его знак характеризует ориентацию деталей в соответствующем блоке ("+" - горизонтальное, "-" - вертикальное).

Конкретная проектная схема выбирается во втором блоке алгоритма. В соответствии с принятым ограничением считаем, что в каждой конкретной схеме раскроя участвуют детали не более двух размеров. Выбор пары размеров деталей для выполнения расчетов происходит в третьем-четвертом блоках алгоритма.

Алгоритм основан на том, что по каждому столбцу и строке матрицы 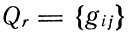строят ограничения на свободные параметры n_i и a_i - модели, затем определяется их оптимальное значение.

В блоках 2-4 выбираются схемы размещения и размеров деталей.

В блоке 7 алгоритма по выбранной матрице Q также определяются векторы V_вi⁽ⁱ¹⁾ и V_гi⁽ⁱ¹⁾ размерностью r, характеризующие участие имеющихся блоков в строках матрицы. Формально это запишется так:

Аналогично в блоке 8 алгоритма определяются векторы σ_вj^(j1) и σ_гj^(j1) характеризующие участие блоков в j-м столбце проектной схемы:

Определив заполнение блоками столбцов и строк выбранной проектной схемы размещения, блок 9 алгоритма производит расстановку выбранных размеров деталей по блокам.

Следующий этап - расчет ограничений на размещение деталей в заданной области - блоки 11 и 12 алгоритма. Для i-й строки

по длине материала

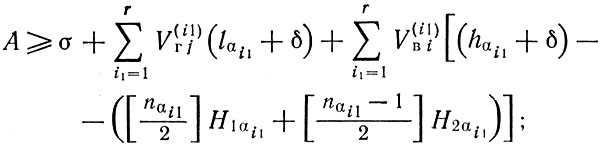
по ширине материала для j-го столбца

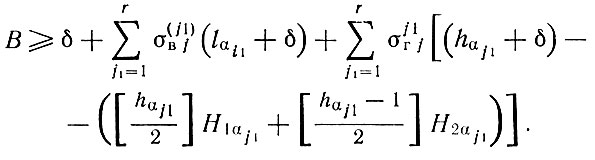
Задача состоит в том, чтобы найти размеры a_i числа деталей n_i, которые удовлетворяли бы приведенным выше условиям и максимизировали процент использования материала:

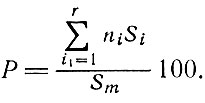
В блоке 13 идет перебор возможных сочетаний размеров деталей с учетом ограничений.

В блоках 14 и 15 происходит расчет процентов использования материала соответственно для горизонтальных Р_г и вертикальных Р_в блоков. После проверки полученного результата на установленное пороговое значение

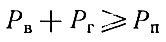
выдается на печать (блок 17 алгоритма). Результат содержит номер проектной схемы размещения, поблочное размещение номеров деталей, процент использования листового материала.

Алгоритм реализован в программу на языке Фортран для ЭВМ серии ЕС. Программа проверена на ассортименте деталей, выпускаемых московским объединением по производству деталей низа обуви "Пролетарий" для подошв мужской обуви Ф-7912261. Размещение производилось на стандартном листе размером 800×600 мм. Так, продолжительность работы ЭВМ ЕС-1020 по выполнению программ поиска экономичных схем размещения колеблется от 1 до 4 мин и зависит от числа блоков введенной проектной схемы.

На пятом уровне методики производится поиск множества возможных экономичных вариантов схем раскроя. Постановка задачи по этому уровню точно такая же, как предыдущая, только добавляется поиск оптимального угла наклона деталей в блоках с подбором соответствующего размера деталей, что позволяет повысить использование площади блока. Алгоритм для решения задачи в этой постановке изображен на рис. 2.30, б с добавлением блоков 1', 5, 6, 10, 17'. Ввод (блок 1' алгоритма) массивы координат среднего размера, коэффициенты приращения по длине и ширине при переходе от номера к номеру, заданный шаг перебора углов наклона, габаритные размеры листового материала, межшаблонный мостик, пороговый процент использования, а также проектные схемы размещения.

В блоках 5 и 6 алгоритма рассчитываются габаритные размеры деталей, линейные эффекты от совмещения деталей в зависимости от изменения угла наклона для выбранных первого и второго размеров.

В блоке 10 алгоритма происходит перебор углов наклона деталей в исходных блоках с целью получения оптимальных количеств деталей и размеров. На печать выдаются полученные значения: процент использования, число деталей в каждом блоке, размеры и угол наклона деталей в каждом блоке.

Алгоритм реализован в программу на языке Фортран для ЭВМ серии ЕС. Работа программы проверена на тех же деталях фасона Ф-7912261. Продолжительность работы программы по поиску множества экономичных вариантов схем раскроя колеблется от 10 до 12 мин в зависимости от числа блоков введенной проектной схемы.

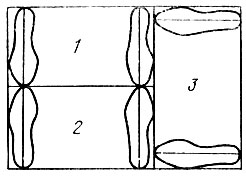
Рис. 2.31. Проектная схема блоков 1-3

Рассмотрим пример применения программы получения экономичных вариантов схем размещения деталей низа обуви на листовых материалах по четвертому уровню методики. Задана проектная схема (рис. 2.31) размещения деталей Ф-7912261. Размер листа 600×800 мм. Нормативный процент использования 76.

В результате счета программы число вариантов-сочетаний размеров, дающих результат выше нормативного, составило 18. Максимальный процент использования (83,78) достигается при таком размещении: блок 1, размер 260 - пять деталей; блок 2, размер 260 - пять деталей; блок 3, размер 245 - шесть деталей.

Рассмотрим пример применения программы получения множества экономичных вариантов схем размещения по пятому уровню методики. Задана проектная схема. Размещаемые детали Ф-7912261. Размер листа 600×800 мм. Нормативный процент использования - 76.

В результате счета программы число вариантов-сочетаний размеров деталей, дающих результат выше нормативного, составило 27. Максимальный процент использования (84,98) достигается при таком размещении: блок 1, размер 260, угол наклона 0° - пять деталей; блок 2, размер 260, угол наклона 0° - пять деталей; блок 3, размер 250, угол наклона 10° - шесть деталей.

Имея множество проектных схем размещения

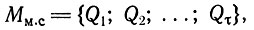
можно по каждой проектной схеме получить n экономичных вариантов. Пусть M(Q_i) - множество экономичных вариантов, полученных из одной проектной схемы Q_i,

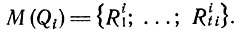
Тогда множество экономичных вариантов схем размещения можно представить так:

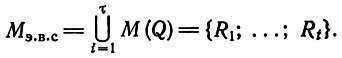
Примем следующие условные обозначения:

i - размер размещаемой детали;

j - номер экономичного варианта раскроя;

X_j - неизвестная, обозначающая, какое количество пластин необходимо раскроить по j-му экономичному варианту;

g_i - количество L деталей, заданное размерным ассортиментом;

r - число размеров, входящих в размерный ассортимент;

t_э - число экономичных вариантов схем раскроя;

S_j - чистая площадь деталей, входящих в j-й экономичный вариант схемы раскроя;

S_i - площадь детали i-ro размера;

m_ij - количество пар i-го размера, выкраиваемых из одной пластины по j-му варианту;

W_i - избыток деталей i-го размера при данном наборе схем размещения;

S_Л - площадь одного листа материала;

F - число используемых листов;

V_i - недостаток деталей i-го размера при данном наборе схем размещения.

Рассмотрим основные условия и ограничения математической модели.

1. Количество размещенных в схемах деталей должно соответствовать заданному размерному ассортименту. Решение должно основываться на условии заменяемости деталей.
   
   (2.43)
   Для детали наибольшего номера в размерном ассортименте условие, обеспечивающее потребность в заданном количестве, будет следующим:
   
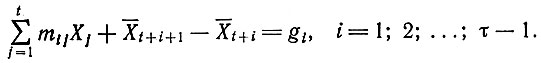
   (2.4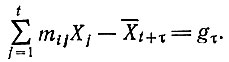4)
2. Полученные решения будут неотрицательными при
   
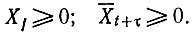
   (2.45)
3. В качестве целевой функции задачи выбираем процент использования материала
   
   
   где S_п - суммарная площадь деталей, размещенных на материале; S'_{и. м} - суммарная площадь используемого материала. Полезную площадь размещенных деталей можно представить в ви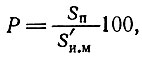де
   
   
   где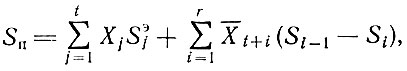 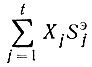- суммарная полезная площадь деталей, размещенных в схемах без учета замен; 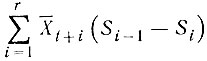- суммарная площадь потерь материала при проведении замен. Исходя из условий (2.43)-(2.45) и соотношения
   
   
   характеризующего чистую площадь деталей, входящих в j-й экономичный вариант, суммарную площадь размещенных деталей можно записать в следующем виде: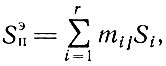
   
   
   Таким образом, S_п является постоянной величиной, поэтому задача максимизации процента использования Р сводится к минимизации суммарной площади используемого материала:
   
   
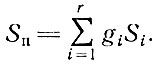   В результате обсуждена возможность применения математической модели [3] для расчета схем размещения деталей низа обуви на листовом материале с учетом заданного размерного ассортимента. Решение данной задачи основано на заменяемости деталей. Исходная информация - экономичные варианты схем размещения деталей получены с помощью методики. Наряду с этим имеется возможность решения поставленной задачи другим методом. Рассмотрим математические модели получения оптимальных схем раскроя деталей низа обуви из листового материала, отличающихся от предыдущих моделей тем, что вводится дополнительное размещение, которое позволит избежать потерь материалов при замене.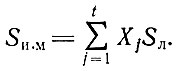

Математическая модель с избытком деталей. Определим и сформулируем ограничения, заложенные в модель.

1. Количество размещенных в схемах деталей должно соответствовать заданному размерному ассортименту:
   
   
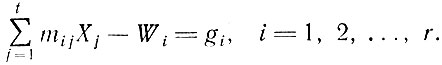
2. Полученные решения будут неотрицательными при
   
   
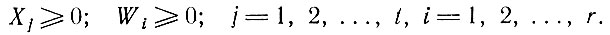
3. В качестве целевой функции выбираем общую площадь материала, занимаемого при размещении всего ассортимента деталей:
   
   
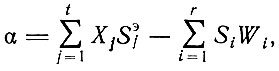
   где 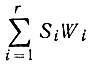- суммарная площадь избыточных деталей. Целевая функция примет вид
   
   
   или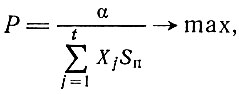
   
   
   Для использования более простых методов решения задач на ЭВМ необходимо привести целевую функцию к линейному виду. Для этого представим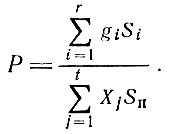
   
   
   
   
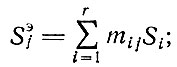   Тогда целевая функция
   
   
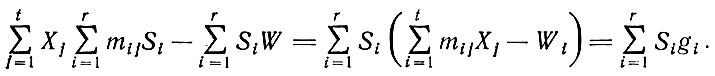   Задача получения схемы раскроя с учетом заданного ассортимента состоит в максимизации использования материала при заданном размерном ассортименте, т. е. для решения задачи требуется максимизировать функционал
   
   
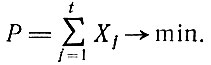   где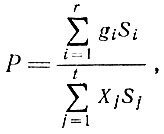 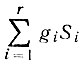- чистая площадь размещенных деталей; 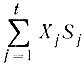- используемая для размещения площадь. Исходя из того что числитель функционала Р в силу постоянства 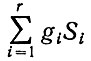будет тоже постоянен, максимизация Р, характеризующая общее число листов используемых материалов, эквивалентна минимизации
   
   

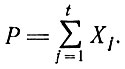
Таблица 2.8. Математическая модель с избытком деталей

Данная модель приведена в табл. 2.8. При решении задачи по этой модели определяется рациональный набор схем размещения деталей низа обуви на листовых материалах, обеспечивающих заданную потребность в деталях различных размеров при максимальном использовании листового материала. Решение осуществляется путем прямого выбора схем раскладок из множества экономичных вариантов, включенных в модель. Полученное решение будет содержать незначительный избыток деталей, а выбранные схемы с размещенными в них деталями будут соответствовать заданному размерному ассортименту. Одним описанным вариантом модели ограничиваться нет необходимости, так как встречаются еще более сложные ситуации.

Математическая модель с недостатком деталей. Опишем ограничения модели и условия ее применения.

1. Условие соблюдения заданного ассортимента деталей:
   
   
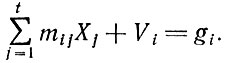
2. Условие неотрицательности полученного решения:
   
   
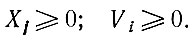
3. Целевую функцию можно представить в виде
   
   
   Целевая функция отражает решение минимизации площади, занимаемой деталями при их размещении с недостатком. Данная модель приведена в табл. 2.9.

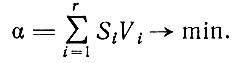
Таблица 2.9. Математическая модель с недостатком деталей

Суть модели заключается в следующем. Сначала выбираются экономичные схемы размещения с числом деталей, которые соответствуют размерному ассортименту или находятся в недостатке по отношению к нему. Определив недостаток деталей (номер и количество), размещают их на листе с повторным поиском оптимального варианта. Полученный таким образом набор схем с размещенными деталями будет соответствовать заданной потребности в деталях.